The Biased Coin Flip
What a simple "heads or tails" can teach us about the market.
There was a talk once given by a hedge fund manager who was a partner at a fund that famously flopped about thirty years ago. As the attendees turned up, they likely expected wisdom, experience, or tales to be shared, but instead, they were offered a coin along with some simple instructions:
You can take out a stake of $25 and bet on the flip of a coin for 30 minutes. The coin is biased to come up heads with a 60% probability, and you can bet as much as you like on heads or tails on each flip. You will be given a check for however much is in your account at the end of the half-hour.
It’s a very simple game, used as an experiment.1 By having participants engage in an activity as simple as flipping a coin, the betting strategy and its evolution can be easily isolated for observation. This simple game also turns out to have properties similar to investing in the stock market, which has implications for finance and economics education.
Strategy and Outcomes
Before falling under the curse of knowledge, what strategy would you approach this game with? Note it down for later.
If you’re a professional gambler, trader or behavioural finance enthusiast, you may have heard of the Kelly criterion. This is the most optimal strategy to approach this simple but intriguing game.
The Kelly formula suggests that a player aiming to maximise the growth rate of their wealth should bet a constant fraction of their total wealth on each coin flip. This fraction is determined by the function 2p - 1, where p represents the probability of winning. The formula assumes that the gambler has logarithmic utility. It makes sense that there is an optimal fraction to bet; if a player wagers a very high percentage, they risk losing a significant amount of money during a losing streak, which could prevent them from recovering. Conversely, if they bet too little, they may not take full advantage of limited opportunities to place bets at favourable odds.
While the expected value of the game increases with the higher fraction a player bets, the outcomes can become so skewed that a risk-averse player will find an optimal betting fraction well below 100%. The odds also influence the optimal fraction to bet; the more favourable the odds, the larger the fraction that should be wagered. Additionally, since the coin flips are independent random outcomes, the strategy should rely solely on the player’s account balance and not on the outcomes of previous flips.
In the game, the Kelly criterion would tell the subject to bet 20% (2*.6-1) of his account on heads on each flip. So, the first bet would be $5 (20% of $25) on heads, and if he won, then he’d bet $6 on heads (20% of $30), but if he lost, he′d bet $4 on heads (20% of $20), and so on.
“How did you go bankrupt? Gradually, and then suddenly.”
— Ernest Hemingway
Although it may seem easy and profitable, with the odds clearly in your favour, many fall short. Over-betting, under-betting, erratic betting (and stupidly betting on tails) are some of the ways that players ultimately lose in the coin flip challenge.
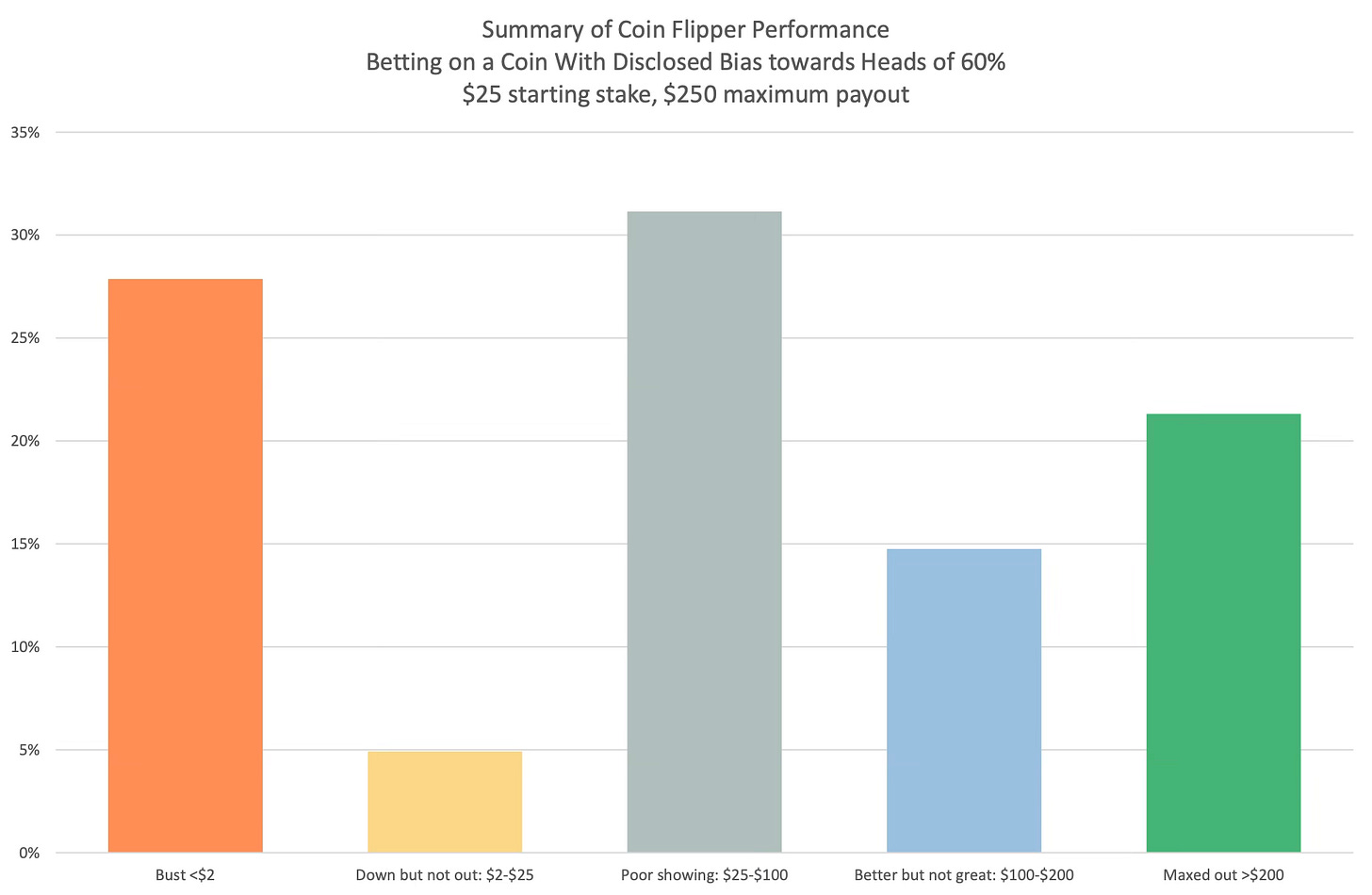
Only 21% of participants reached the maximum payout of $250, well below the 95% who should have, given a simple constant percentage betting strategy of 10% to 20%.
Surprising? Most would say so. That a game of flipping coins with an ex-ante 60/40 winning probability produced so many subjects that lost everything (28%) is startling.
The average ending bankroll of the 51% of the sample who did not reach the maximum and who did not go bust was $75. While this was a tripling of their initial $25 stake, it still represents a very sub-optimal outcome, given the opportunity presented.
Of the 61 subjects, 18 subjects bet their entire bankroll on one flip, which increased the probability of ruin from close to 0% using Kelly to 40% if their all-in flip was on heads or 60% if they bet it all on tails, which amazingly some of them did. (If you take one thing away from this article, it’s to not be in that group.)
An additional finding from the study indicated that a notable number of participants believed that employing a Martingale betting strategy, characterised by increasing wager sizes following losses, was an optimal approach. Conversely, several subjects adopted a strategy of placing small and consistent wagers, seemingly aiming to minimise the risk of financial ruin while maximising the likelihood of achieving a profitable outcome.
Finally, 67% of the participants bet on tails at some point during the experiment. 48% bet on tails more than five times in the game. It is possible that some of these subjects questioned whether the coin truly had a 60% bias towards heads, but that hypothesis is not supported by the fact that within the subset of 13 subjects who bet on tails more than 25% of the time, we found they were more likely to make that bet right after the arrival of a string of heads. That could suggest that some combination of the illusion of control, law of small numbers bias, gamblers fallacy or hot hand fallacy was at work.
In the Markets
If you gave an investor the next day′s news 24 hours in advance, he would go bust in less than a year.
— Nassim Taleb
It’s a grand experiment that we can learn a lot from. But what are the takeaways for trading the markets? There are a lot of similarities. The real return of US equities over the past 50 years was a bit over 5%, and the annual standard deviation was about 15%, giving a return/risk ratio of about 0.33. Many market observers believe the prospective return/risk ratio of the stock market is well below its historical average and closer to that of our coin flip opportunity, which has a return/risk ratio of 0.2.
Of course, there are significant differences, from the binary versus continuous nature of outcomes to the question of risk versus uncertainty when investing in the stock market, where no one can tell you the distribution from which you will draw outcomes. Further, most investors believe the stock market is not a successive set of independent flips of a coin but that there are elements of mean reversion and trending in stock market behaviour. Of course, outlier events happen with a much higher probability than would evolve from a series of coin flips.
The behavioural learnings from this are the best applications. Even with the odds in your favour (akin to having an edge in the markets), the amount you bet plays a key role. Too little, and you’ll sell yourself short. Too much, and you can blow it all quicker than you realise. How much you bet based on the opportunity should be part of your strategy. Oh, and never go “all in” on one trade.
Another takeaway is regarding what you bet on. Please never bet on tails; that goes without saying. The market translation would be to avoid low-probability trades. Maybe that is a short-dated option, where theta decay works as a headwind. Maybe it’s small, cheap stocks or cryptos that you view as get-rich-quick wildcards. Whatever it may be, that’s for you to decide and not the topic of today’s article. But know what your “tail” bets are, and avoid them.
Keep emotions in control. That’s always important. The traders that increased bets after losing streaks (often muttered as “doubling down”) usually led to decreased performance. Sticking to a rational investing or trading system leads to longevity in the market. That may be hard initially, as markets can be whipsaw, but it’s vital.
It’s time to return to our question. What strategy did you decide on? And was it different to the Kelly criterion you would (hopefully) now employ?
Now, you might be reading this and want to try this experiment/game for yourself. We’ve got your back. Here it is.
Support for our writings is always appreciated. If you’d like to share this with others, please feel free. Leaving a like or comment is also very helpful (tell us your results if you try the game).
Happy betting,
AlphaPicks
“Rational Decision-Making Under Uncertainty: Observed Betting Patterns on a Biased Coin” by Victor Haghani and Richard Dewey, 2016.




Thanks for sharing! Very interesting